HashMap源码的细节与启发
1. 前言
这些天心血来潮想认认真真过一遍JCF的源码实现,在阅读到HashMap的时候发现自己之前还是太肤浅,很多地方没能理解JDK作者的巧思,因此想记录下来自己学习过程中的收获。
在正式开始之前先吹一波美团技术团队,之前看并发编程的时候也是搜到不少美团技术团队的文章,写的既专业又接地气,这次看HashMap也多亏美团技术团队写的文章:《Java 8系列之重新认识HashMap》
2. 哈希表
首先,HashMap其实是**哈希表(Hash table,又被称为散列表)的一种实现,哈希表是根据关键码值(Key value)而直接进行访问的数据结构。**
哈希表中,指定的关键码值Key通过哈希函数(散列函数)运算后可以得到当前关键字的记录在表中的地址。
构造散列函数一般有如下方法:

在哈希表中,尽管可以选取一个比较好的哈希函数,但**哈希冲突无法避免,我理解为Key值通过哈希函数计算得到的哈希值相同,称为哈希冲突**。
解决哈希冲突的方法有很多,这里笔者摘录维基百科中的两种方案为例:
- 开放寻址法(包括线性探测,平方探测,伪随机探测等):

- 冲突链表法(单独链表法):

哈希表的查找过程中,关键码的比较次数,取决于产生冲突的多少,产生的冲突少,查找效率就高,产生的冲突多,查找效率就低。因此,影响产生冲突多少的因素,也就是影响查找效率的因素。影响产生冲突多少有以下三个因素:
- 列函数是否均匀
- 处理冲突的方法
- 散列表的载荷因子(load factor)
载荷因子:

3. HashMap的底层数据结构
HashMap其实是基于哈希桶算法实现的哈希表,底层数据结构为数组 + 链表的形式。
这里借一张计算所的小鼠标大佬的图:

左边是HashMap的哈希桶数组,代码中如下定义:
//HashMap的属性
transient Node<K,V>[] table;
//Node节点的定义
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
//略......
}
从代码中我们可以看到,Node节点通过Node.next构建了一个链表结构,正如上图右半部分所画的那样。
需要注意的是在JDK1.8中,HashMap引入了红黑树来改善HashMap的查询效率,代码如下:
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
TreeNode<K,V> parent; // red-black tree links
TreeNode<K,V> left;
TreeNode<K,V> right;
TreeNode<K,V> prev; // needed to unlink next upon deletion
boolean red;
}
红黑树(R-B Tree)是一种自平衡的BST(二叉查找树),时间复杂度是O(logn),优于一般的二叉查找数O(n)的时间复杂度,也更加稳定。但是,红黑树的插入删除节点是比较麻烦的,需要经过左旋(逆时针),右旋(顺时针),变色这些方法来辅助完成。关于红黑树这里就不进行展开了。
在JDK1.8中,当哈希桶的某一位置的链表长度大于8,HashMap会重构当前位置的普通链表(基于Node类)为红黑树链表(基于TreeNode)。
除此以外,在HashMap中还有一些重要的成员属性也需要了解:
- size : HashMap当前容纳的键值对数量。
- threshold : 翻译过来是阀值的意思,就是HashMap所能容纳的最大键值对数量。
- loadFactor : 负载因子(载荷因子),一般取默认值
DEFAULT_LOAD_FACTOR,也就是0.75,一般不建议修改这个值。
哈希桶数组(table),负载因子(loadFactor),阀值(threshold)满足下列关系式:
table.length * loadFactor = threshold
这个关系式与哈希表中定义是一致的。
笔者认为,HashMap中用的哈希桶算法本质上依然是通过冲突链表法(单独链表)来解决哈希冲突,所谓的哈希桶只是规定哈希表的长度的一种方式,发生了哈希冲突也还是通过一个链表来排列所有哈希冲突的值。当然这里笔者没有查到更多的资料,只是按照自己的知识储备去理解。
4. HashMap使用的散列函数(哈希函数)
根据上文我们知道,HashMap作为哈希表的实现,是通过一个散列函数来确定哈希桶数组的索引位置的。
HashMap使用如下散列函数,即:
//hash值 与 哈希表长度-1
f(x) = hash(key) & (table.length - 1)
HashMap对散列函数其实本质上就是使用对除留余数法,这里创造JDK的大师们用了非常巧妙的方法将求余运算转化为了位运算中的与运算,提高了性能。
下文具体说明这个优化。
4.1. HashMap的hash()方法
我们知道,Java中每个对象都会有Object的方法**#{hashCode}**,这个可以在我们写类的时候进行重写,之后我们来看下HashMap#hash()源码:
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
引用美团技术团队的一句话,不做深入探讨:
(h = k.hashCode()) ^ (h »> 16),主要是从速度、功效、质量来考虑的,这么做可以在数组table的length比较小的时候,也能保证考虑到高低Bit都参与到Hash的计算中,同时不会有太大的开销。
4.2. HashMap哈希桶长度固定为2的次幂
HashMap的长度(即哈希桶数组长度length)固定为2的次幂,这一点可以从HashMap#resize()方法看出:
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
//老的长度左移1位,也就是扩大2倍
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1;
}
else if (oldThr > 0)
//oldCap为0,取oldThr阀值,这个值是在初始化的时候赋值,也是会保证是2的次幂
newCap = oldThr;
else {
//默认值1 << 4,即16,也是2的次幂
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
//newCap肯定是2的次幂,初始化哈希桶
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
//略......
}
也就是说,哈希桶长度取值有以下可能:
- 初始化赋值的threshold值
- 初始长度左移N位
后面一个是2的次幂没有疑问,关于初始化赋值的threshold值,我们看初始化调用的代码:
static final int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
这个方法保证了32位的int类型的threshold值肯定会是2的次幂,这个需要试几个例子就会明白,其实就是将这个数字第一个为1的位右边的二进制位全部置0,最后通过+1得到一个2的次幂,这里不展开叙述。
最终,我们得出结论,HashMap的哈希桶长度一定是2的次幂。
4.3. 求模运算转化为位运算
我们认为,在哈希桶数组长度(table.length)为2的次幂时,会有以下等式:
//true
h & (table.length -1) == h % table.length
本质上,因为table.length - 1 与 h 做与运算等于将h的高位全部置0,也就实现了快速求余的效果。
与运算效率优于求模运算,性能得以提升。
5. JDK8的优化与JDK7中的死循环问题
5.1. JDK7中的多线程死循环问题
在JDK7中,多个线程同时执行put方法,有可能出现死循环,我们从代码中分析:
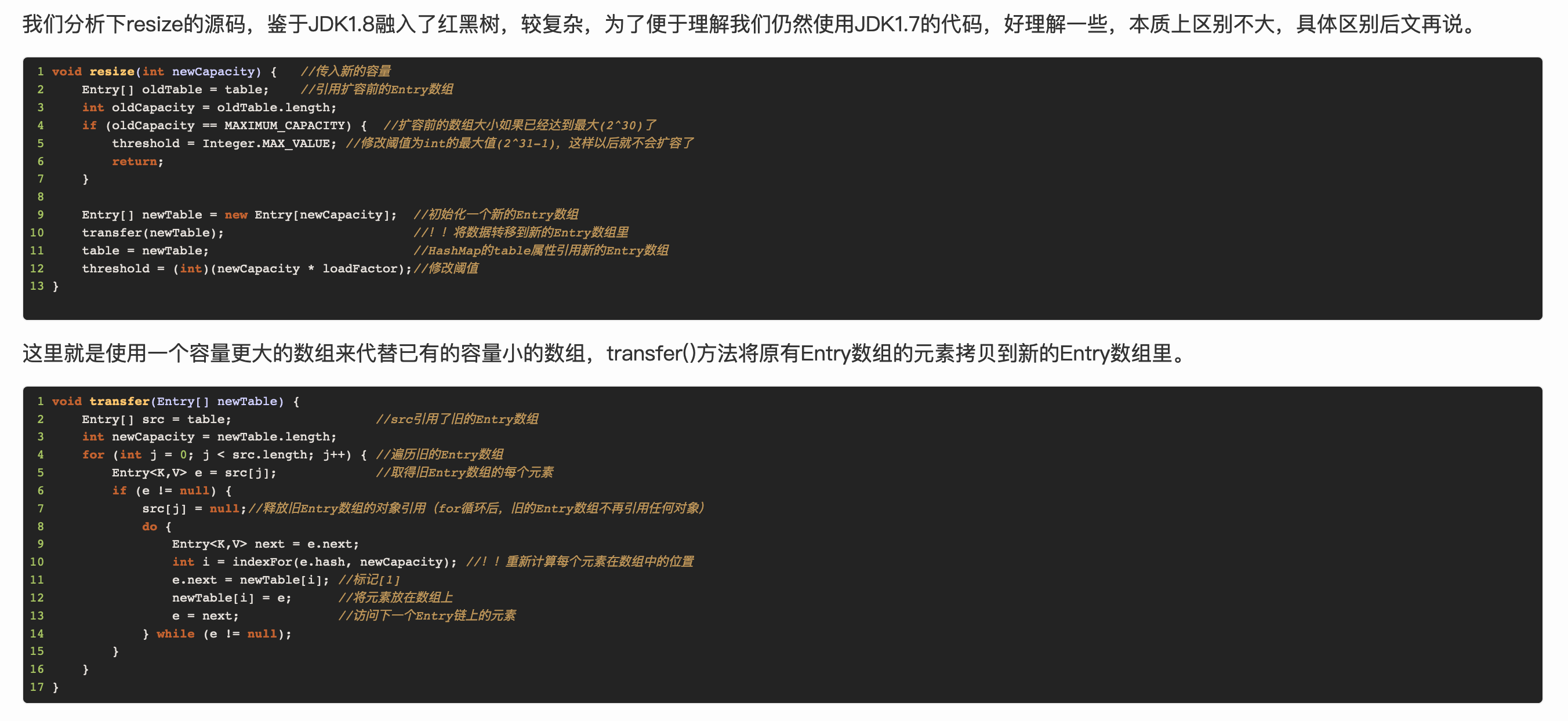
这里可以看到,JDK7采用的是头插法进行插入,会有两个问题:
- 链表的顺序会被改变(改为倒序)
- 多个线程执行时,有可能会导致链表最后一个元素指向第一个元素,进而导致这个链表无限循环遍历,也就是图中
#transfer()方法。
5.2. JDK8的优化
JDK8对HashMap有很多的优化,这里主要举两个主要的变化:
5.2.1. 引入红黑树
当哈希桶某个位置链表数量大于8时,会调用HashMap#treefy()方法将链表转化为红黑树,进而提升查找性能:
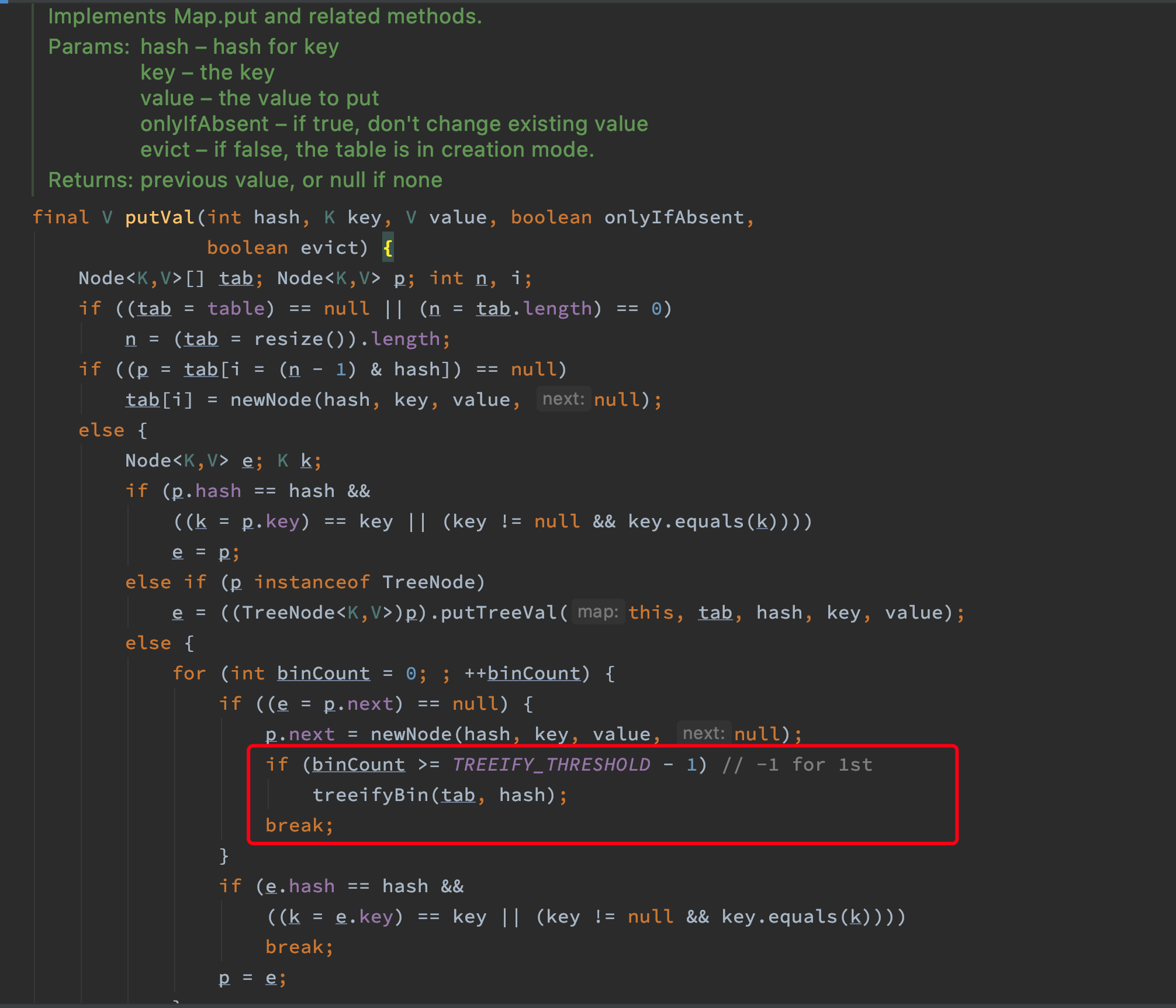
5.2.2. 优化重构哈希桶的算法
在JDK8中,HashMap#resize()方法通过双指针进行移动,取代了头插法,会保持链表的顺序。
这里看一下双指针的执行逻辑,其实很有意思:
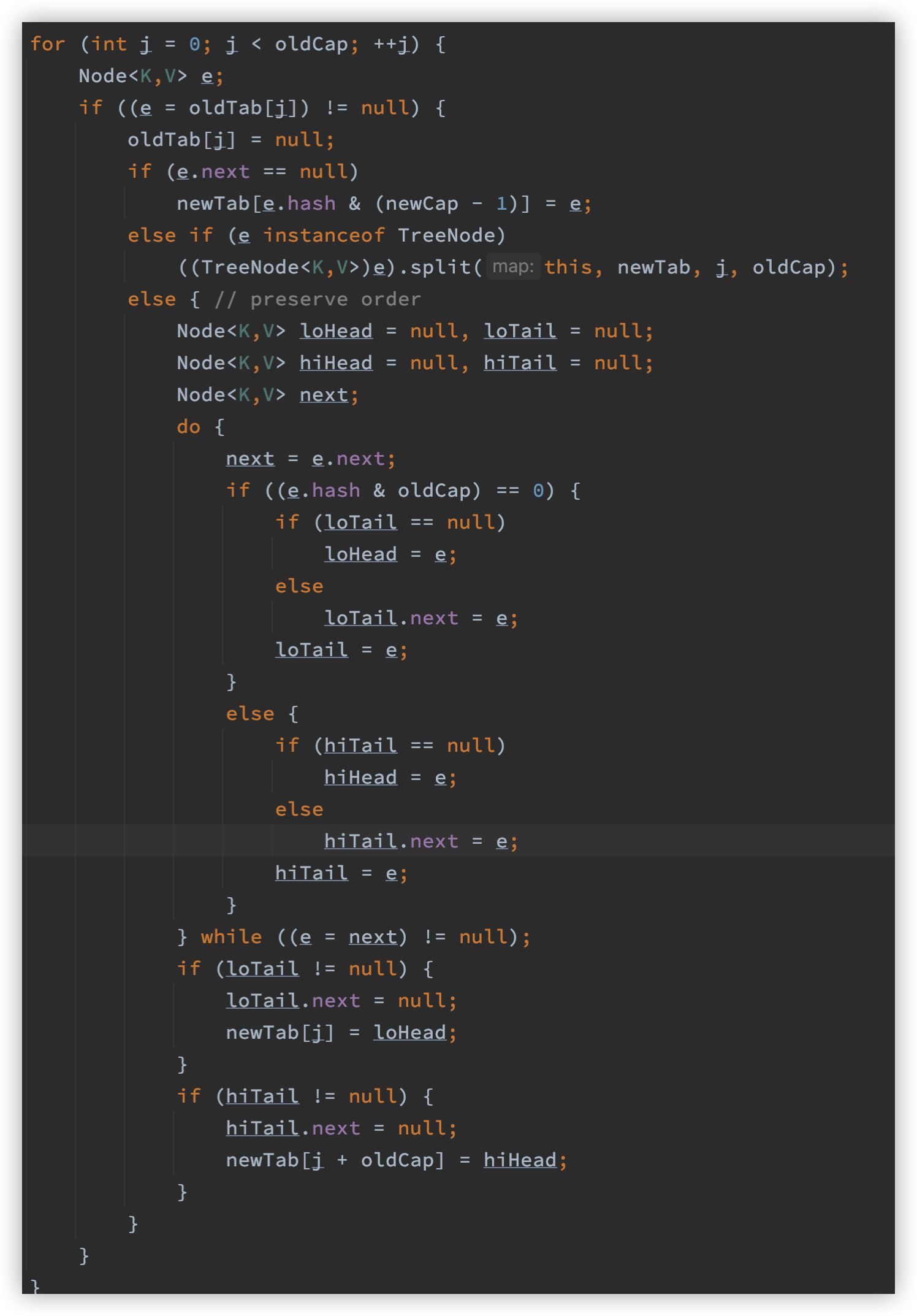
这一段代码笔者也是参考了很多文章才能理解,我们先给一些先入为主的结论:
- lo开头的对象,比如
loHead和loTail,其实是保存了前后哈希桶位置没有变化的数据链表 - hi开头的对象,比如
hiHead和hiTail,其实是保存了前后哈希桶会变化的数据链表。
结合代码,这里有两个问题:
-
为什么
e.hash & oldCap == 0就可以认为哈希桶位置不需要位移? -
为什么需要位移的数据,需要位移j个长度?
newTab[j + oldCap] = hiHead
我们看一些实际的例子,假设现在hash值为27,长度从8 → 16
我们知道,哈希桶的位置基于以下算式:
hash & (n - 1)
哈希值不会变,resize前后的区别其实是受n的改变而变化。
具体来看,计算这个例子中哈希数组位置,有以下计算:
// 计算原来的位置,hash & (n-1)
27 - 011011
7 - 000111
hash & (n-1) = 27 & 7 = 000011 = 3
// 计算resize后的位置,hash & (n-1)
27 - 011011
16 - 001111
hash & (n-1) = 27 & 16 = 001011 = 11
可以看到,本质上,是否变化取决于这里n - 1的第4位,第4位的值从0→1。
我们知道,只要与0做与运算,结果就不会发生变化,因此哈希桶位置是否变化取决于hash值的第4位。
再进一步说,这里的第4位是否为0,其实就是 hash & 原来的n 是否为0,而新的位置其实就等于原位置 +原来的n 。
这个推导不够严谨,但是我们基本可以有以下结论:
- resize后的哈希桶位置是否要发生变化,取决于
hash & 原长度是否为0,是则不变。 - resize后的哈希桶位置如果发生变化,新位置 =
原长度 + 原位置。
有这个特性其实是因为n的特性:
- n也就是长度,一定是2的次幂
- 每次resize是执行
newCap = oldCap << 1,只移动一位
JDK8的resize优化采用双指针不改变顺序的方式避免了老版本头插法顺序的改变带来头尾连接,最终招致死循环的问题。
6. 构造函数入参
HashMap提供了好几种重载的构造方法,可以自定义容量,负载因子等。
-
关于容量,需要注意的是,由于HashMap会调整容量从初始的16到大于16的2的次幂数,所以入参的参数并不是HashMap真正的容量。
除此以外,从上文
HashMap#resize()的源码也可以看出,重构哈希桶的损耗和算法是很复杂的,代价很高,因此如果能在一开始确认长度也可指定一下长度避免多次resize的性能损耗。容量的设置举个例子:比如现在需要1000个数放入HashMap
假设我们使用下面代码进行初始化:
Map map = new HashMap(1000);之后经过
tableSizeFor()方法,最终threshold会变赋值为1024,看起来是足够,但是在实际put值的时候,threshold值会受负载因子的影响,被改变为1024 * 0.75 = 768,这个需要跟一下put方法就可以看到,最终不能够满足需求,因此需要计算:1000/负载因子 = 1000/0.75 = 1333.3333......最后,我们需要至少大于1333的2的次幂数,即2048就是我们需要的初始容量。
-
关于负载因子,美团技术团队是如下解释的:
默认的负载因子0.75是对空间和时间效率的一个平衡选择,建议大家不要修改,除非在时间和空间比较特殊的情况下,如果内存空间很多而又对时间效率要求很高,可以降低负载因子Load factor的值;相反,如果内存空间紧张而对时间效率要求不高,可以增加负载因子loadFactor的值,这个值可以大于1。